Why Phi-4 14B Is So Much Better Than GPT-4o And o1 — Here The Results
Welcome to the world of AI, where I present you with the latest content focused on developers and AI technology enthusiasts. I help you understand technology trends and innovative products
In this Story, we’re diving into some of the latest AI developments from major players like Phi-4, GPT-4o, and o1
On January 7, 2024, Microsoft released the Small Language Model (SLM) “Phi-4” on Hugging Face. This model is provided under the MIT license and can be freely used and modified for commercial use.
Phi-4 is the latest model in Microsoft’s “Phi” series, and while it is lightweight, it has excellent performance in certain fields. In particular, it has shown accuracy that exceeds large-scale language models (LLMs) in mathematical reasoning and is attracting attention for its use in specialized tasks.
Phi-4 improves accuracy through high-quality data and new post-training technology and has been released to Azure AI Foundry and Hugging Face.
The model size is 14B, and if it is a 4-bit quantized model, it should run on a decent GPU. The minimum model of Meta’s Llama3.2 and Google’s Gemma2, both open models, is 1B and 2B, respectively, so this is more than one size larger.
I’m not sure what Microsoft’s definition of “small” is, but in any case, it is something that can be used openly and easily.
In this step-by-step guide, we will cover what Phi-4 is, What are the special features of Phi-4, how to use Phi-4 locally, and why it performs better than LLM
Before we start! 🦸🏻♀️
If you like this topic and you want to support me:
like my article; that will really help me out.👏
Follow me on my YouTube channel
Subscribe to me to get the latest article.
What is Phi-4
Phi-4 is an attempt to show a different approach to conventional AI models. It is characterized by its relatively small number of parameters of 14 billion while demonstrating superior performance compared to large-scale AI models such as Google’s Gemini Pro 1.5.
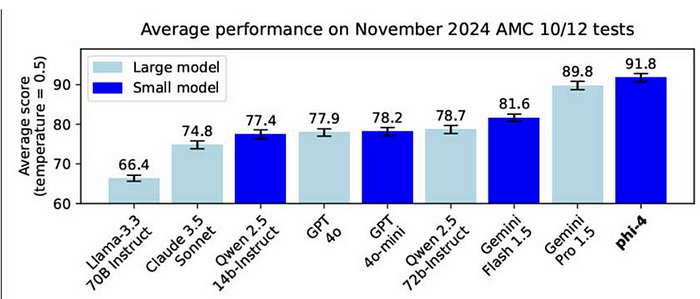
What has attracted particular attention is its high mathematical reasoning ability. At the American Mathematical Competition (AMC) hosted by the American Mathematical Association (MAA), Phi-4 outperformed large-scale models in problems that required logical thinking, such as solving complex equations and mathematical proofs.
This result shows the possibility of use in fields where accurate numerical calculations are essential, such as scientific research, engineering, and financial modeling.
What are the special features of Phi-4?
Phi-4 benchmark test results are as follows:
It scored over 80% in the MATH and MGSM tests, surpassing Google Gemini Pro and OpenAI’s GPT-4o-mini.
Excellent performance in mathematical reasoning skills is important in finance, engineering, and scientific research.
The programmed HumanEval performed well on benchmark tests.
In addition, the Phi-4 architecture and training process strongly emphasise precision and efficiency. Its 14-billion-parameter decoder-only transformer model is trained on a total of 9.8 trillion tokens from orchestrated and synthetic datasets.
In terms of training methods, the Microsoft team used supervised fine-tuning and direct preference optimization (DPO) methods to ensure solid performance and solve issues such as fairness and stability.
Microsoft emphasizes that the Phi-4 training process considers responsible AI development and undergoes extensive security assessments, including attack testing, to reduce the risk of bias, harmful content, and false information.
Install Locally
The model in Hugging Face is quite large, about 30GB, and it is a bit difficult to run it on my machine.
I was wondering if I could somehow make it run on my machine by applying 4-bit quantization or something, and I found that Ollama had a model that was already quantized to Q4_K_M, so I was grateful to borrow it and would like to share the work notes I took with it.
Download
ollama run phi4Note: When the downloaded model is expanded into memory, it will be a little over 10GB in size, so if you are running it on a CPU, you will need at least that much free memory space, and if you are running it on a GPU, you will need at least that much GPU memory otherwise you will get an error.
If the model is downloaded successfully, you should see the following prompt:
>>> Send a message (/? for help)When you see this prompt, try sending a message. If you’re using a GPU-accelerated environment, you’ll probably get a pretty quick response.
>>> Hello!
Hello! Please let me know how I can assist you. If you have any questions, feel free to ask.
>>> Send a message (/? for help)With just this, I can now use the Phi-4 locally! This is very helpful.
Now you can easily run Phi-4 on your own machine using Ollama! It even comes with a REST API!
This means that a model with performance equivalent to an LLM with around 70B parameters can be run on a portable PC, and Ollama’s REST API function can quickly set up an environment where it can be called locally from other applications and libraries. I’m looking forward to making use of this in various ways in the future.
Phi-4 vs GPT-4o vs and o1
let’s compare o1 and GPT-4o and verify how much performance Phi-4 has.
Next, I would like to present some applied problems and verify whether the results differ from those of the LLMs GPT-4o and o1 and whether they are simpler.
The application problems to be examined are as follows:
Calculate the 20th value of the following sequence: 1, 1, 2, 3, 5, 8, ….
A bank offers an annual interest rate of 5%, compounded semi-annually. What is the final amount if 1 million dollars is deposited for 10 years?
If the volume of a rectangular prism is 120 cubic centimetres, its height is 6 cm, and its width is 4 cm, what is its length?
Question 1: will test your accuracy, simplicity, and response time.
Question 2: will test your accuracy in calculating interest rates
Question 3: will test your geometric reasoning skills.
Next, let’s try solving this problem and enter the following into the prompt:
The sequence given is the Fibonacci sequence, where each term is the sum of the two preceding ones, starting with 1 and 1. The first few terms are:
( F_1 = 1 )
( F_2 = 1 )
( F_3 = F_1 + F_2 = 1 + 1 = 2 )
( F_4 = F_2 + F_3 = 1 + 2 = 3 )
( F_5 = F_3 + F_4 = 2 + 3 = 5 )
( F_6 = F_4 + F_5 = 3 + 5 = 8 )
We need to find the 20th term, ( F_{20} ).
Continuing the sequence:
( F_7 = F_5 + F_6 = 5 + 8 = 13 )
( F_8 = F_6 + F_7 = 8 + 13 = 21 )
( F_9 = F_7 + F_8 = 13 + 21 = 34 )
( F_{10} = F_8 + F_9 = 21 + 34 = 55 )
( F_{11} = F_9 + F_{10} = 34 + 55 = 89 )
( F_{12} = F_{10} + F_{11} = 55 + 89 = 144 )
( F_{13} = F_{11} + F_{12} = 89 + 144 = 233 )
( F_{14} = F_{12} + F_{13} = 144 + 233 = 377 )
( F_{15} = F_{13} + F_{14} = 233 + 377 = 610 )
( F_{16} = F_{14} + F_{15} = 377 + 610 = 987 )
( F_{17} = F_{15} + F_{16} = 610 + 987 = 1597 )
( F_{18} = F_{16} + F_{17} = 987 + 1597 = 2584 )
( F_{19} = F_{17} + F_{18} = 1597 + 2584 = 4181 )
( F_{20} = F_{18} + F_{19} = 2584 + 4181 = 6765 )
Thus, the 20th value of the sequence is ( \boxed{6765} ).Phi-4
The sequence given is the Fibonacci sequence, where each term is the sum of the two preceding ones, starting with 1 and 1. The first few terms are:
( F_1 = 1 )
( F_2 = 1 )
( F_3 = F_1 + F_2 = 1 + 1 = 2 )
( F_4 = F_2 + F_3 = 1 + 2 = 3 )
( F_5 = F_3 + F_4 = 2 + 3 = 5 )
( F_6 = F_4 + F_5 = 3 + 5 = 8 )
We need to find the 20th term, ( F_{20} ).
Continuing the sequence:
( F_7 = F_5 + F_6 = 5 + 8 = 13 )
( F_8 = F_6 + F_7 = 8 + 13 = 21 )
( F_9 = F_7 + F_8 = 13 + 21 = 34 )
( F_{10} = F_8 + F_9 = 21 + 34 = 55 )
( F_{11} = F_9 + F_{10} = 34 + 55 = 89 )
( F_{12} = F_{10} + F_{11} = 55 + 89 = 144 )
( F_{13} = F_{11} + F_{12} = 89 + 144 = 233 )
( F_{14} = F_{12} + F_{13} = 144 + 233 = 377 )
( F_{15} = F_{13} + F_{14} = 233 + 377 = 610 )
( F_{16} = F_{14} + F_{15} = 377 + 610 = 987 )
( F_{17} = F_{15} + F_{16} = 610 + 987 = 1597 )
( F_{18} = F_{16} + F_{17} = 987 + 1597 = 2584 )
( F_{19} = F_{17} + F_{18} = 1597 + 2584 = 4181 )
( F_{20} = F_{18} + F_{19} = 2584 + 4181 = 6765 )
Thus, the 20th value of the sequence is ( \boxed{6765} ).GPT-4o
The sequence given is the **Fibonacci sequence**, where each term is the sum of the two preceding terms:
\[F(n) = F(n-1) + F(n-2) \quad \text{for } n \geq 3\]
with \( F(1) = 1 \) and \( F(2) = 1 \).
We need to compute the **20th value** of this sequence.
The first few terms are:
1. \( F(1) = 1 \)
2. \( F(2) = 1 \)
3. \( F(3) = 2 \)
4. \( F(4) = 3 \)
5. \( F(5) = 5 \)
6. \( F(6) = 8 \)
7. \( F(7) = 13 \)
8. \( F(8) = 21 \)
9. \( F(9) = 34 \)
10. \( F(10) = 55 \)
11. \( F(11) = 89 \)
12. \( F(12) = 144 \)
13. \( F(13) = 233 \)
14. \( F(14) = 377 \)
15. \( F(15) = 610 \)
16. \( F(16) = 987 \)
17. \( F(17) = 1597 \)
18. \( F(18) = 2584 \)
19. \( F(19) = 4181 \)
20. \( F(20) = 6765 \)
Thus, the 20th value in the sequence is: 6765o1
The given sequence is the Fibonacci sequence, defined by:
\[F_1 = 1, \quad F_2 = 1, \quad \text{and} \quad F_{n} = F_{n-1} + F_{n-2} \text{ for } n > 2.\]
To find the 20th term, let's list them out (or recall the known values):
1. \( F_1 = 1 \)
2. \( F_2 = 1 \)
3. \( F_3 = 2 \)
4. \( F_4 = 3 \)
5. \( F_5 = 5 \)
6. \( F_6 = 8 \)
7. \( F_7 = 13 \)
8. \( F_8 = 21 \)
9. \( F_9 = 34 \)
10. \( F_{10} = 55 \)
11. \( F_{11} = 89 \)
12. \( F_{12} = 144 \)
13. \( F_{13} = 233 \)
14. \( F_{14} = 377 \)
15. \( F_{15} = 610 \)
16. \( F_{16} = 987 \)
17. \( F_{17} = 1597 \)
18. \( F_{18} = 2584 \)
19. \( F_{19} = 4181 \)
20. \( F_{20} = 6765 \)
Therefore, the 20th value in the sequence is: 6765All the models can give the correct answer, but Phi-4’s way of solving is good for people who don’t have a strong math background. There isn’t much difference in the time it takes to get the answer.
Let’s try to solve the second question and use this prompt in your chatbot
A bank offers an annual interest rate of 5%, compounded semi-annually.
What is the final amount if 1 million dollar is deposited for 10 years?Phi-4
To calculate the final amount when interest is compounded semi-annually, we can use the compound interest formula:
[ A = P \left(1 + \frac{r}{n}\right)^{nt} ]
where:
( A ) is the final amount
( P ) is the principal amount (initial deposit)
( r ) is the annual interest rate (in decimal form)
( n ) is the number of times the interest is compounded per year
( t ) is the number of years
For this problem:
( P = 1,000,000 ) dollars
( r = 0.05 ) (5% as a decimal)
( n = 2 ) (compounded semi-annually)
( t = 10 ) years
Plugging the values into the formula:
[ A = 1,000,000 \left(1 + \frac{0.05}{2}\right)^{2 \times 10} ]
[ A = 1,000,000 \left(1 + 0.025\right)^{20} ]
[ A = 1,000,000 \times (1.025)^{20} ]
Now, calculate ( (1.025)^{20} ):
[ (1.025)^{20} \approx 1.638616 ]
Therefore:
[ A \approx 1,000,000 \times 1.638616 ]
[ A \approx 1,638,616 ]
The final amount after 10 years is approximately $1,638,616.GPT-4o
To calculate the final amount with compound interest, you can use the formula:
\[ A = P \left(1 + \frac{r}{n}\right)^{nt} \]
where:
- \( A \) is the final amount,
- \( P \) is the principal amount (initial deposit),
- \( r \) is the annual nominal interest rate (as a decimal),
- \( n \) is the number of times the interest is compounded per year,
- \( t \) is the number of years.
Given:
- \( P = 1,000,000 \) dollars,
- \( r = 0.05 \) (5%),
- \( n = 2 \) (since the interest is compounded semi-annually),
- \( t = 10 \).
Plug these values into the formula:
\[ A = 1,000,000 \left(1 + \frac{0.05}{2}\right)^{2 \times 10} \]
\[ A = 1,000,000 \left(1 + 0.025\right)^{20} \]
\[ A = 1,000,000 \times (1.025)^{20} \]
Now calculate \( (1.025)^{20} \):
\[ (1.025)^{20} \approx 1.6386164403 \]
Now find the final amount \( A \):
\[ A \approx 1,000,000 \times 1.6386164403 \]
\[ A \approx 1,638,616.44 \]
The final amount after 10 years will be approximately \$1,638,616.44.o1
To calculate the final amount for a \$1,000,000 deposit with an annual interest rate of 5% compounded semi-annually over 10 years, you can use the compound interest formula:
\[
A = P \left(1 + \frac{r}{n}\right)^{nt}
\]
Where:
- \( A \) = the amount of money accumulated after n years, including interest.
- \( P \) = the principal amount (\$1,000,000).
- \( r \) = the annual interest rate (decimal) (5% or 0.05).
- \( n \) = the number of times that interest is compounded per year (2 for semi-annually).
- \( t \) = the time the money is invested for in years (10).
Plugging in the values:
\[
A = 1,000,000 \times \left(1 + \frac{0.05}{2}\right)^{2 \times 10} = 1,000,000 \times (1.025)^{20}
\]
Calculating \( (1.025)^{20} \):
\[
(1.025)^{20} \approx 1.63862
\]
Now, multiply this by the principal:
\[
A \approx 1,000,000 \times 1.63862 = 1,638,620
\]
**Final Amount:** After 10 years, the investment will grow to approximately **\$1,638,620**.All the models were able to get the correct results. O1 is significantly faster than the other models, completing the task in just 11.38 ms.GPT-4o and Phi-4 are much slower, with Phi-4 taking slightly longer than GPT-4o.
Reasoning
Finally, we are going to test a test of geometric reasoning ability. please use this prompt in your chatbot
If the volume of a rectangular prism is 120 cubic centimetres,
its height is 6 cm, and its width is 4 cm, what is its length?Phi-4
To find the length of the rectangular prism, we can use the formula for the volume of a rectangular prism:
[ \text{Volume} = \text{Length} \times \text{Width} \times \text{Height} ]
Given:
Volume = 120 cubic centimeters
Height = 6 cm
Width = 4 cm
Substitute the known values into the formula:
[ 120 = \text{Length} \times 4 \times 6 ]
Simplify the equation:
[ 120 = \text{Length} \times 24 ]
To solve for the Length, divide both sides by 24:
[ \text{Length} = \frac{120}{24} ]
Calculate the division:
[ \text{Length} = 5 ]
Thus, the length of the rectangular prism is 5 cm.GPT-4o
To find the length of the rectangular prism, you can use the formula for the volume of a rectangular prism:
\[ \text{Volume} = \text{length} \times \text{width} \times \text{height} \]
You are given the volume (120 cubic centimeters), the height (6 cm), and the width (4 cm). Plug these values into the formula:
\[ 120 = \text{length} \times 4 \times 6 \]
First, calculate \(4 \times 6\):
\[ 120 = \text{length} \times 24 \]
Next, solve for the length by dividing both sides of the equation by 24:
\[ \text{length} = \frac{120}{24} \]
\[ \text{length} = 5 \]
Thus, the length of the rectangular prism is 5 centimeters.o1
To find the **length** of the rectangular prism, you can use the formula for the volume of a rectangular prism:
\[
\text{Volume} = \text{Length} \times \text{Width} \times \text{Height}
\]
Given:
- **Volume (V)** = 120 cubic centimetres (cm³)
- **Height (h)** = 6 centimetres (cm)
- **Width (w)** = 4 centimetres (cm)
**Step 1: Write down the formula with the known values.**
\[
120 = \text{Length} \times 4 \times 6
\]
**Step 2: Simplify the equation to solve for Length.**
\[
\text{Length} = \frac{120}{4 \times 6}
\]
\[
\text{Length} = \frac{120}{24}
\]
\[
\text{Length} = 5 \text{ cm}
\]
**Answer:** The length of the rectangular prism is **5 centimetres**.All the models gave the correct results, but O1 and Phi-4 are better at reasoning. They solve problems step by step, like how a human would think. I am surprised that GPT-4o is not as good at reasoning as O1 and Phi-4.
Conclusion :
I compared Phi-4 with GPT-4o and O1 and saw that the speed was almost the same. Phi-4 is open-source, and I like open-source more than GPT-4o and O1. Even though O1 was much faster and better, I will stick with Phi-4. I don’t see a big difference between Phi-4 and the other Models, and Phi-4 is small enough to run on my laptop, which is very important since I don’t have a powerful computer.
🧙♂️ I am an AI Generative expert! If you want to collaborate on a project, drop an inquiry here or Book a 1-on-1 Consulting Call With Me.